4 Regresja

4.1 Wprowadzenie

Metody regresji pozwalają na analizowanie zależności przyczynowo-skutkowych oraz predycję nieznanych wartości. Korzystając z tej metody należy jednak pamiętać, że model regresji jest tylko przybliżeniem rzeczywistości.

Przykłady zastosowania regresji:

zależność wielkości sprzedaży od wydatków na reklamę
zależność wynagrodzenia od lat doświadczenia

Na początku pracy wczytujemy biblioteki tidyverse i readxl.

library(tidyverse)
library(readxl)

4.2 Regresja prosta

Na podstawie danych dotyczących informacji o doświadczeniu i wynagrodzeniu pracowników zbuduj model określający ‘widełki’ dla potencjalnych pracowników o doświadczeniu równym 8, 10 i 11 lat.

Wczytujemy dane i sprawdzamy czy nie występują zera bądź braki danych z użyciem funkcji summary().

salary <- read_xlsx("data/salary.xlsx")

summary(salary)

 YearsExperience      Salary      
 Min.   : 1.100   Min.   : 37731  
 1st Qu.: 3.200   1st Qu.: 56721  
 Median : 4.700   Median : 65237  
 Mean   : 5.313   Mean   : 76003  
 3rd Qu.: 7.700   3rd Qu.:100545  
 Max.   :10.500   Max.   :122391

Następnie stworzymy wykres.

plot(salary)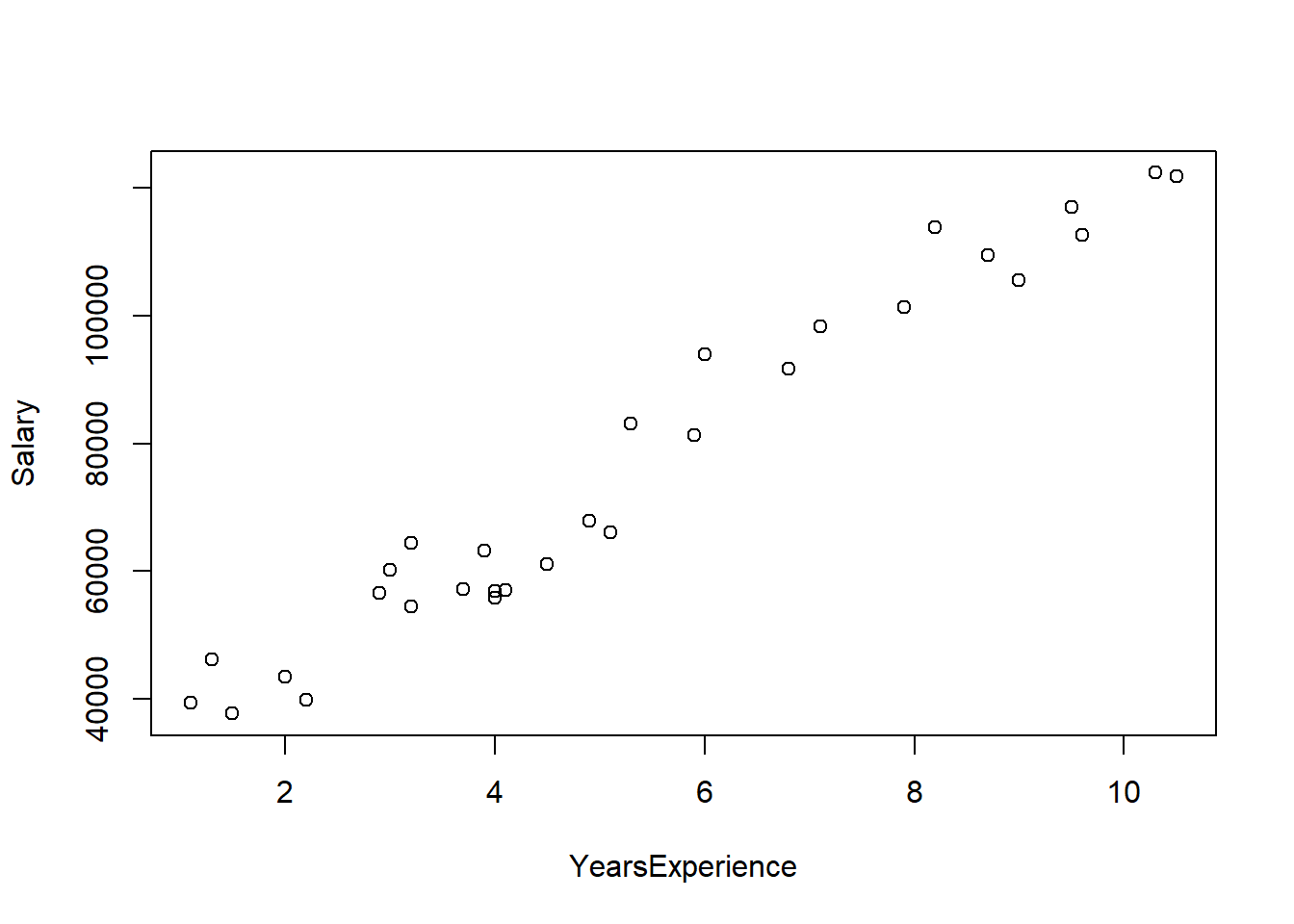

Najprostszym sposobem wizualizacji jest wykorzystanie funkcji plot(), niemniej taki wykres nie jest najpiękniejszy i trudno się go formatuje. Dużo lepiej skorzystać z pakietu ggplot2.

ggplot(salary, aes(x=YearsExperience, y=Salary)) + 
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  xlab("Doświadczenie") + 
  ylab("Pensja") +
  xlim(0,12) +
  ylim(35000, 126000) +
  theme_bw()

`geom_smooth()` using formula = 'y ~ x'

W argumentach funkcji ggplot() podajemy co wizualizujemy, natomiast sposób prezentacji ustalany jest przez funkcje geom. Funkcje xlab() i ylab() określają etykiety osi, a xlim() i ylim() wartości graniczne. Funkcje rozpoczynające się od theme_ określają wygląd wykresu.

Modelowanie rozpoczynamy od określenia zmiennej zależnej i niezależnej.

zmienna zależna/objaśniana: pensja - $y$
zmienna niezależna/objaśniająca: doświadczenie - $x$

Szukamy teraz wzoru na prostą opisującą badane cechy.

Ogólna postać regresji prostej jest następująca:

\[\hat{y}_{i}=b_{1}x_{i}+b_{0}\]

gdzie $\hat{y}$ oznacza wartość teoretyczną, leżącą na wyznaczonej prostej, $x_i$ wartość zmiennej niezależnej, a $b_1$ i $b_0$ to współczynniki modelu.

Wobec tego wartości empiryczne $y$ będą opisane formułą:

\[y_{i}=b_{1}x_{i}+b_{0}+u_{i}\]

w której $u_i$ oznacza składnik resztowy wyliczany jako $u_{i}=y_{i}-\hat{y}_{i}$.

Współczynnik kierunkowy $b_1$ informuje o ile przeciętne zmieni się wartość zmiennej objaśnianej $y$, gdy wartość zmiennej objaśniającej $x$ wzrośnie o jednostkę.

Wyraz wolny $b_0$ to wartość zmiennej objaśnianej $y$, w sytuacji w której wartość zmiennej objaśniającej $x$ będzie równa 0. Często interpretacja tego parametru nie ma sensu.

Następnie w R korzystamy z funkcji lm, w której należy określić zależność funkcyjną w formie: zmienna_zalezna ~ zmienna niezalezna.

salary_model <- lm(formula = Salary ~ YearsExperience, data = salary)
summary(salary_model)


Call:
lm(formula = Salary ~ YearsExperience, data = salary)

Residuals:
    Min      1Q  Median      3Q     Max 
-7958.0 -4088.5  -459.9  3372.6 11448.0 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)      25792.2     2273.1   11.35 5.51e-12 ***
YearsExperience   9450.0      378.8   24.95  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5788 on 28 degrees of freedom
Multiple R-squared:  0.957, Adjusted R-squared:  0.9554 
F-statistic: 622.5 on 1 and 28 DF,  p-value: < 2.2e-16

Na podstawie otrzymanego wyniku dokonujemy interpretacji parametrów.

b1 = 9450 - wzrost doświadczenia o rok powoduje przeciętny wzrost pensji o 9450 $
b0 = 25792,2 - pracownik o doświadczeniu 0 lat uzyska pensję w wysokości 25792,2 $

Trzy gwiazki przy współczynniku $b_1$ oznaczają, że doświadczenie ma istotny wpływ na wartości pensji. Wyraz wolny także jest istotny, natomiast ogólnie nie jest wymagana jesgo istotność.

Oprócz interpretacji współczynników ważne są jeszcze inne miary jakości modelu.

Odchylenie standardowe składnika resztowego jest pierwiastkiem z sumy kwadratów reszt podzielonej przez liczbę obserwacji pomniejszoną o 2:

\[S_{u}=\sqrt{\frac{\sum\limits_{i=1}^{n}{(y_{i}-\hat{y}_{i})^2}}{n-2}}\]

Błąd resztowy (odchylenie standardowe składnika resztowego) $S_u$ wynosi 5788$, co oznacza, że wartości obliczone na podstawie modelu różnią się od rzeczywistości średnio o +/- 5788$

Współczynnik determinacji określa, jaki procent wariancji zmiennej objaśnianej został wyjaśniony przez funkcję regresji. $R^2$ przyjmuje wartości z przedziału $<0;1>$ ( $<0\%;100\%>$ ), przy czym model regresji tym lepiej opisuje zachowanie się badanej zmiennej objaśnianej, im $R^2$ jest bliższy jedności (bliższy 100%)

\[R^2=1-\frac{\sum\limits_{i=1}^{n}{(y_{i}-\hat{y}_{i})^2}}{\sum\limits_{i=1}^{n}{(y_{i}-\bar{y}_{i})^2}}\]

Współczynnik $R^2$ (multiple R-squared) wynosi 0,957 czyli doświadczenie wyjaśnia 95,7% zmienności pensji

Na podstawie tego modelu dokonamy wyznaczenia wartości teoretycznych dla kilku wybranych wartości doświadczenia. Nowe wartości muszą być w postaci zbioru danych, zatem tworzymy nową ramkę danych.

nowiPracownicy <- data.frame(YearsExperience=c(8,10,11))

predict(salary_model, nowiPracownicy)

       1        2        3 
101391.9 120291.8 129741.8

Tym sposobem uzyskujemy następujące widełki:

pracownik o 8 latach doświadczenia - proponowana pensja 101391,9 $ +/- 5788 $
pracownik o 10 latach doświadczenia - proponowana pensja 120291,8 $ +/- 5788 $
pracownik o 11 latach doświadczenia - proponowana pensja 129741,8 $ +/- 5788 $

W powyższym przykładzie prognozowane wartości pojawiły się w konsoli, natomiast w sytuacji, w której chcielibyśmy wykonać predykcję dla bardzo wielu nowych wartości to warto te prognozowane wartości umieścić od razu w zbiorze danych. Można to zrobić w następujący sposób:

nowiPracownicy <- nowiPracownicy %>% 
  mutate(salary_pred=predict(object = salary_model, newdata = .))

nowiPracownicy

  YearsExperience salary_pred
1               8    101391.9
2              10    120291.8
3              11    129741.8

W powyższym kodzie symbol . oznacza analizowany zbiór danych, zatem nie ma potrzeby powtarzania jego nazwy.

4.2.1 Zadanie

Dla danych dotyczących sklepu nr 77 opracuj model zależności sprzedaży od liczby klientów. Ile wynosi teoretyczna sprzedaż w dniach, w których liczba klientów będzie wynosiła 560, 740, 811 oraz 999 osób?

4.3 Regresja wieloraka

Ogólna postać regresji wielorakiej jest następująca:

\[\hat{y}_{i}=b_{1}x_{1i}+b_{2}x_{2i}+...+b_{k}x_{ki}+b_{0}\]

W tym przypadku nie wyznaczamy prostej tylko $k$-wymiarową przestrzeń.

Na podstawie danych dotyczących zatrudnienia opracuj model, w którym zmienną zależną jest bieżące wynagrodzenie. Za pomocą regresji określimy jakie cechy mają istotny wpływ na to wynagrodzenie.

Opis zbioru:

id - kod pracownika
plec - płeć pracownika (0 - mężczyzna, 1 - kobieta)
data_urodz - data urodzenia
edukacja - wykształcenie (w latach nauki)
kat_pracownika - grupa pracownicza (1 - specjalista, 2 - menedżer, 3 - konsultant)
bwynagrodzenie - bieżące wynagrodzenie
pwynagrodzenie - początkowe wynagrodzenie
staz - staż pracy (w miesiącach)
doswiadczenie - poprzednie zatrudnienie (w miesiącach)
zwiazki - przynależność do związków zawodowych (0 - nie, 1 - tak)
wiek - wiek (w latach)

Rozpoczynamy od wczytania danych,

pracownicy <- read_xlsx("data/pracownicy.xlsx")

pracownicy2 <- pracownicy %>%
  filter(!is.na(wiek)) %>%
  select(-id, -data_urodz) %>%
  mutate(plec=as.factor(plec),
         kat_pracownika=as.factor(kat_pracownika),
         zwiazki=as.factor(zwiazki))

summary(pracownicy2)

 plec       edukacja     kat_pracownika bwynagrodzenie   pwynagrodzenie 
 0:257   Min.   : 8.00   1:362          Min.   : 15750   Min.   : 9000  
 1:216   1st Qu.:12.00   2: 27          1st Qu.: 24000   1st Qu.:12450  
         Median :12.00   3: 84          Median : 28800   Median :15000  
         Mean   :13.49                  Mean   : 34418   Mean   :17009  
         3rd Qu.:15.00                  3rd Qu.: 37050   3rd Qu.:17490  
         Max.   :21.00                  Max.   :135000   Max.   :79980  
      staz       doswiadczenie    zwiazki      wiek      
 Min.   :63.00   Min.   :  0.00   0:369   Min.   :24.00  
 1st Qu.:72.00   1st Qu.: 19.00   1:104   1st Qu.:30.00  
 Median :81.00   Median : 55.00           Median :33.00  
 Mean   :81.14   Mean   : 95.95           Mean   :38.67  
 3rd Qu.:90.00   3rd Qu.:139.00           3rd Qu.:47.00  
 Max.   :98.00   Max.   :476.00           Max.   :66.00

W zmiennej wiek występował brak danych, który został usunięty. Usunięto także kolumny, które nie przydadzą się w modelowaniu. Ponadto dokonujemy przekształcenia typu cech, które są jakościowe (płeć, kat_pracownika, zwiazki) z typu liczbowego na czynnik/faktor. Taka modyfikacja powoduje, że ta cecha będzie przez model traktowana jako zmienna dychotomiczna (zerojedynkowa). Proces trasformacji takiej cechy jest pokazany poniżej.

Oryginalny zbiór

id	stanowisko
1	specjalista
2	menedżer
3	specjalista
4	konsultant
5	konsultant

Zmienna zerojedynkowa

id	menedżer	konsultant
1	0	0
2	1	0
3	0	0
4	0	1
5	0	1

W modelu zmienna zależna to bwynagrodzenie, natomiast jako zmienne niezależne bierzemy pod uwagę wszystkie pozostałe cechy. W celu uniknięcia notacji naukowej w uzyskiwanych wynikach dodajemy opcję options(scipen = 5).

options(scipen = 5)

model <- lm(bwynagrodzenie ~ ., pracownicy2)
summary(model)


Call:
lm(formula = bwynagrodzenie ~ ., data = pracownicy2)

Residuals:
   Min     1Q Median     3Q    Max 
-23185  -3041   -705   2591  46295 

Coefficients:
                   Estimate  Std. Error t value Pr(>|t|)    
(Intercept)     -4764.87418  3590.49652  -1.327  0.18514    
plec1           -1702.43743   796.51779  -2.137  0.03309 *  
edukacja          482.43603   160.83977   2.999  0.00285 ** 
kat_pracownika2  6643.17910  1638.06138   4.056 5.87e-05 ***
kat_pracownika3 11169.64519  1372.73990   8.137 3.77e-15 ***
pwynagrodzenie      1.34021     0.07317  18.315  < 2e-16 ***
staz              154.50876    31.65933   4.880 1.46e-06 ***
doswiadczenie     -15.77375     5.78369  -2.727  0.00663 ** 
zwiazki1        -1011.55276   787.80884  -1.284  0.19978    
wiek              -64.78787    47.88015  -1.353  0.17668    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6809 on 463 degrees of freedom
Multiple R-squared:  0.8444,    Adjusted R-squared:  0.8414 
F-statistic: 279.1 on 9 and 463 DF,  p-value: < 2.2e-16

Tak zbudowany model wyjaśnia 84,4% zmienności bieżącego wynagrodzenia, ale nie wszystkie zmienne są w tym modelu istotne.

Parametry regresji mają następujące interpretacje:

plec1 - kobiety zarabiają przeciętnie o 1702,44 zł mniej niż mężczyźni,
edukacja - wzrost liczby lat nauki o rok powoduje średni wzrost bieżącego wynagrodzenia o 482,44 zł
kat_pracownika2 - pracownicy o kodzie 2 (menedżer) zarabiają średnio o 6643,18 zł więcej niż pracownik o kodzie 1 (specjalista)
kat_pracownika2 - pracownicy o kodzie 3 (konsultant) zarabiają średnio o 11169,65 zł więcej niż pracownik o kodzie 1 (specjalista)
pwynagrodzenie - wzrost początkowego wynagrodzenia o 1 zł powoduje przeciętny wzrost bieżącego wynagrodzenia o 1,34 zł
staz - wzrost stażu pracy o miesiąc skutkuje przeciętnym wzrostem bieżącego wynagrodzenia o 154,51 zł
doswiadcznie - wzrost doświadczenia o miesiąc powoduje średni spadek bieżącego wynagrodzenia o 15,77 zł
zwiazki1 - pracownicy należący do związków zawodowych zarabiają średnio o 1011,55 zł mniej aniżeli pracownicy, którzy do związków nie zależą
wiek - wzrost wieku pracownika o 1 rok to przeciętnym spadek bieżącego wynagrodzenia o 64,79 zł

Wszystkie te interpretacje obowiązują przy założeniu ceteris paribus - przy pozostałych warunkach niezmienionych.

Ten model wymaga oczywiście ulepszenia do czego wykorzystamy pakiet olsrr.

Pierwszą kwestią, którą się zajmiemy jest współliniowość zmiennych. W regresji zmienne objaśniające powinny być jak najbardziej skorelowane ze zmienną objaśnianą, a możliwie nieskorelowane ze sobą. W związku z tym wybieramy ze zbioru wyłącznie cechy ilościowe, dla którym wyznaczymy współczynnik korelacji liniowej Pearsona. Do wizualizacji tych wartości wykorzystamy pakiet corrplot służący do wizualizacji współczynnika korelacji.

library(corrplot)
library(olsrr)

korelacje <- pracownicy2 %>%
  select(-c(plec, kat_pracownika, zwiazki)) %>%
  cor()

corrplot(korelacje, method = "number", type = "upper")

Możemy zauważyć, że wartości bieżącego wynagrodzenia są najsilniej skorelowane w wartościami wynagrodzenia początkowego. Także doświadczenie i wiek są silnie ze sobą związane, co może sugerować, że obie zmienne wnoszą do modelu podobną informację.

W związku z tym powinniśmy wyeliminować niektóre zmienne z modelu pozostawiając te najważniejsze. Wyróżnia się trzy podejścia do tego zagadnienia:

ekspercki dobór cech,
budowa wszystkich możliwych modeli i wybór najlepszego według określonego kryterium,
regresja krokowa.

W przypadku budowy wszystkich możliwych modeli należy pamiętać o rosnącej wykładniczo liczbie modeli: $2^p-1$, gdzie $p$ oznacza liczbę zmiennych objaśniających. w rozważanym przypadku liczba modeli wynosi 255.

wszystkie_modele <- ols_step_all_possible(model)

W uzyskanym zbiorze danych są informacje o numerze modelu, liczbie użytych zmiennych, nazwie tych zmiennych oraz wiele miar jakości. Te, które warto wziąć pod uwagę to przede wszystkim:

rsquare - współczynnik R-kwadrat,
aic - kryterium informacyjne Akaike,
msep - błąd średniokwadratowy predykcji.

Najwyższa wartość współczynnika $R^2$ związana jest z modelem zawierającym wszystkie dostępne zmienne objaśniające. Jest to pewna niedoskonałość tej miary, która rośnie wraz z liczbą zmiennych w modelu, nawet jeśli te zmienne nie są istotne.

W przypadku kryteriów informacyjnych oraz błędu średniokwadratowego interesują nas jak najmniejsze wartości. Wówczas jako najlepszy należy wskazać model nr 219 zawierający 6 zmiennych objaśniających.

Metodą, która także pozwoli uzyskać optymalny model, ale przy mniejszym obciążeniu obliczeniowym jest regresja krokowa polegająca na krokowym budowaniu modelu.

ols_step_both_aic(model)


                                    Stepwise Summary                                    
--------------------------------------------------------------------------------------
Step    Variable                 AIC          SBC         SBIC        R2       Adj. R2 
--------------------------------------------------------------------------------------
 0      Base Model            10565.472    10573.790    9220.060    0.00000    0.00000 
 1      pwynagrodzenie (+)     9862.260     9874.737    8518.596    0.77484    0.77436 
 2      kat_pracownika (+)     9786.152     9806.947    8440.801    0.80992    0.80870 
 3      doswiadczenie (+)      9743.487     9768.441    8398.512    0.82705    0.82557 
 4      staz (+)               9719.469     9748.582    8374.863    0.83630    0.83455 
 5      edukacja (+)           9707.338     9740.610    8363.030    0.84112    0.83907 
 6      plec (+)               9703.188     9740.620    8359.065    0.84317    0.84081 
--------------------------------------------------------------------------------------

Final Model Output 
------------------

                             Model Summary                              
-----------------------------------------------------------------------
R                          0.918       RMSE                   6762.202 
R-Squared                  0.843       MSE                46514089.581 
Adj. R-Squared             0.841       Coef. Var                19.815 
Pred R-Squared             0.837       AIC                    9703.188 
MAE                     4418.325       SBC                    9740.620 
-----------------------------------------------------------------------
 RMSE: Root Mean Square Error 
 MSE: Mean Square Error 
 MAE: Mean Absolute Error 
 AIC: Akaike Information Criteria 
 SBC: Schwarz Bayesian Criteria 

                                      ANOVA                                        
----------------------------------------------------------------------------------
                        Sum of                                                    
                       Squares         DF        Mean Square       F         Sig. 
----------------------------------------------------------------------------------
Regression    116287161827.859          7    16612451689.694    357.149    0.0000 
Residual       21629051655.016        465       46514089.581                      
Total         137916213482.875        472                                         
----------------------------------------------------------------------------------

                                         Parameter Estimates                                           
------------------------------------------------------------------------------------------------------
          model         Beta    Std. Error    Std. Beta      t        Sig          lower        upper 
------------------------------------------------------------------------------------------------------
    (Intercept)    -6547.147      3402.860                 -1.924    0.055    -13234.036      139.741 
 pwynagrodzenie        1.342         0.073        0.618    18.382    0.000         1.198        1.485 
kat_pracownika2     6734.992      1631.122        0.092     4.129    0.000      3529.708     9940.275 
kat_pracownika3    11226.635      1368.413        0.251     8.204    0.000      8537.596    13915.674 
  doswiadczenie      -22.302         3.571       -0.137    -6.246    0.000       -29.318      -15.285 
           staz      147.865        31.461        0.087     4.700    0.000        86.041      209.689 
       edukacja      501.391       160.270        0.085     3.128    0.002       186.447      816.335 
          plec1    -1878.949       761.703       -0.055    -2.467    0.014     -3375.755     -382.143 
------------------------------------------------------------------------------------------------------

Otrzymany w ten sposób model jest tożsamy z modelem charakteryzującym się najlepszymi miarami jakości spośród zbioru wszystkich możliwych modeli:

wybrany_model <- lm(bwynagrodzenie ~ pwynagrodzenie + kat_pracownika + doswiadczenie + staz + plec + edukacja, data = pracownicy2)
summary(wybrany_model)


Call:
lm(formula = bwynagrodzenie ~ pwynagrodzenie + kat_pracownika + 
    doswiadczenie + staz + plec + edukacja, data = pracownicy2)

Residuals:
   Min     1Q Median     3Q    Max 
-22922  -3300   -673   2537  46524 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)     -6547.147   3402.860  -1.924  0.05496 .  
pwynagrodzenie      1.342      0.073  18.382  < 2e-16 ***
kat_pracownika2  6734.992   1631.122   4.129 4.32e-05 ***
kat_pracownika3 11226.635   1368.413   8.204 2.30e-15 ***
doswiadczenie     -22.302      3.571  -6.246 9.51e-10 ***
staz              147.865     31.461   4.700 3.43e-06 ***
plec1           -1878.949    761.703  -2.467  0.01399 *  
edukacja          501.391    160.270   3.128  0.00187 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6820 on 465 degrees of freedom
Multiple R-squared:  0.8432,    Adjusted R-squared:  0.8408 
F-statistic: 357.1 on 7 and 465 DF,  p-value: < 2.2e-16

Uzyskany model charakteryzuje się nieznacznie większym błędem resztowym od modelu ze wszystkimi zmiennymi, ale wszystkie zmienne są istotne. Wyraz wolny (Intercept) nie musi być istotny w modelu.

Wróćmy jeszcze na chwilę do tematu współliniowości zmiennych objaśniających:

ols_vif_tol(wybrany_model)

        Variables Tolerance      VIF
1  pwynagrodzenie 0.2979792 3.355939
2 kat_pracownika2 0.6867111 1.456217
3 kat_pracownika3 0.3595692 2.781106
4   doswiadczenie 0.7054176 1.417600
5            staz 0.9862198 1.013973
6           plec1 0.6831049 1.463904
7        edukacja 0.4607529 2.170361

Współczynnik tolerancji wskazuje na procent niewyjaśnionej zmienności danej zmiennej przez pozostałe zmienne objaśniające. Przykładowo współczynnik tolerancji dla początkowego wynagrodzenia wynosi 0,2980, co oznacza, że 30% zmienności początkowego wynagrodzenia nie jest wyjaśnione przez pozostałe zmienne w modelu. Z kolei współczynnik VIF jest obliczany na podstawie wartości współczynnika tolerancji i wskazuje o ile wariancja szacowanego współczynnika regresji jest podwyższona z powodu współliniowości danej zmiennej objaśniającej z pozostałymi zmiennymi objaśniającymi. Wartość współczynnika VIF powyżej 4 należy uznać za wskazującą na współliniowość. W analizowanym przypadku takie zmienne nie występują.

Ocena siły wpływu poszczególnych zmiennych objaśniających na zmienną objaśnianą w oryginalnej postaci modelu nie jest możliwa. Należy wyznaczyć standaryzowane współczynniki beta, które wyliczane są na danych standaryzowanych, czyli takich, które są pozbawione jednostek i cechują się średnią równą 0, a odchyleniem standardowym równym 1. Standaryzacja ma sens tylko dla cech numerycznych, w związku z czym korzystamy z funkcji mutate_if(), która jako pierwszy argument przyjmuje warunek, który ma być spełniony, aby była zastosowane przekształcenie podawane jako drugi argument.

pracownicy2_std <- pracownicy2 %>%
  mutate_if(is.numeric, scale)

wybrany_model_std <- lm(bwynagrodzenie ~ pwynagrodzenie + kat_pracownika + 
                          doswiadczenie + staz + plec + edukacja, data = pracownicy2_std)
summary(wybrany_model_std)


Call:
lm(formula = bwynagrodzenie ~ pwynagrodzenie + kat_pracownika + 
    doswiadczenie + staz + plec + edukacja, data = pracownicy2_std)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.34098 -0.19306 -0.03939  0.14841  2.72171 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)     -0.08893    0.03144  -2.828  0.00488 ** 
pwynagrodzenie   0.61842    0.03364  18.382  < 2e-16 ***
kat_pracownika2  0.39400    0.09542   4.129 4.32e-05 ***
kat_pracownika3  0.65677    0.08005   8.204 2.30e-15 ***
doswiadczenie   -0.13657    0.02187  -6.246 9.51e-10 ***
staz             0.08691    0.01849   4.700 3.43e-06 ***
plec1           -0.10992    0.04456  -2.467  0.01399 *  
edukacja         0.08464    0.02706   3.128  0.00187 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.399 on 465 degrees of freedom
Multiple R-squared:  0.8432,    Adjusted R-squared:  0.8408 
F-statistic: 357.1 on 7 and 465 DF,  p-value: < 2.2e-16

Spośród cech ilościowych największy wpływ na zmienną objaśnianą mają wartości wynagrodzenia początkowego, staż, edukacja i na końcu doświadczenie.

Reszty czyli różnice pomiędzy obserwowanymi wartościami zmiennej objaśnianej, a wartościami wynikającymi z modelu w klasycznej metodzie najmniejszych kwadratów powinny być zbliżone do rozkładu normalnego. Oznacza to, że najwięcej reszt powinno skupiać się wokół zerowych różnic, natomiast jak najmniej powinno być wartości modelowych znacznie różniących się od tych rzeczywistych.

ols_plot_resid_hist(wybrany_model)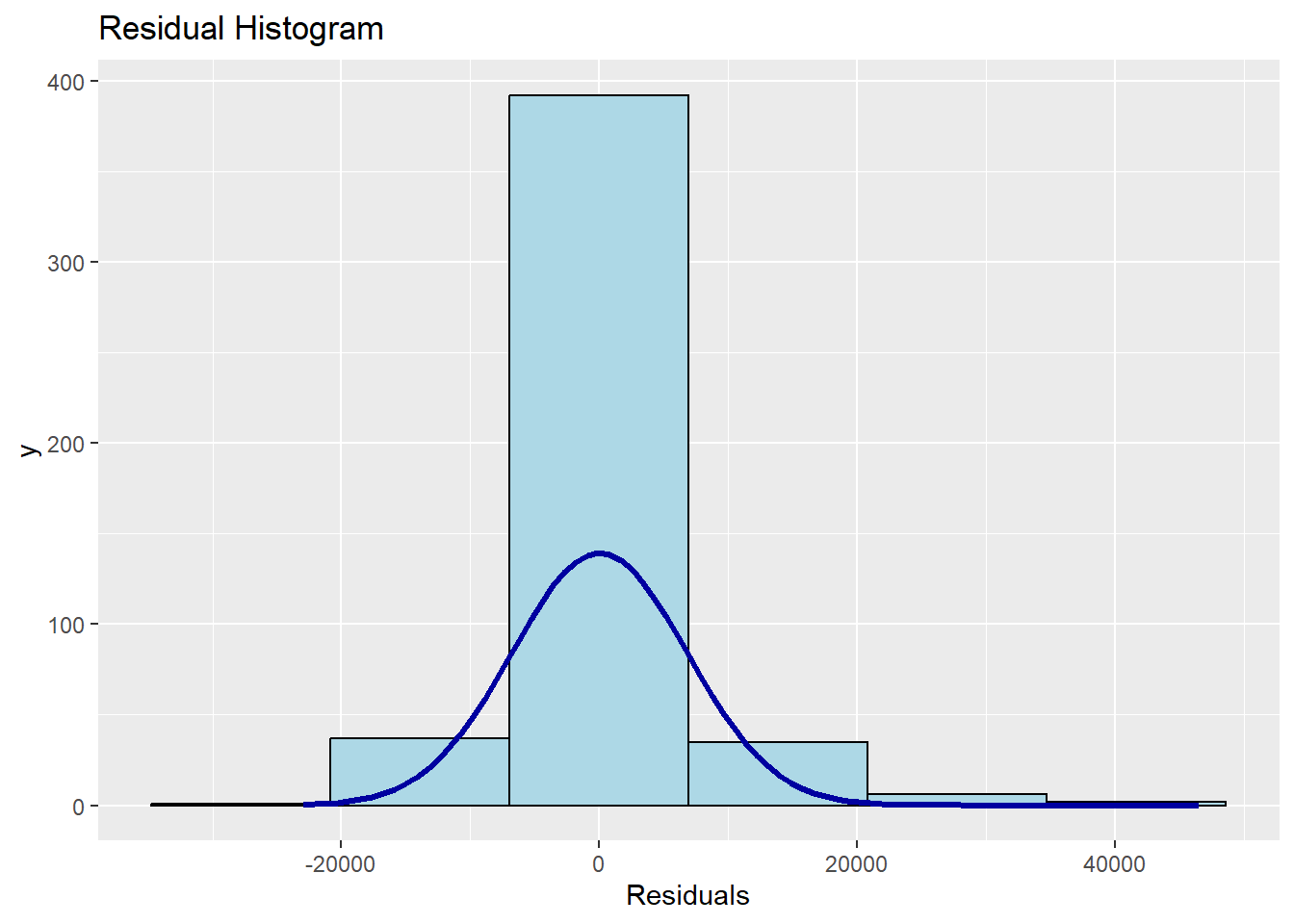

Reszty w naszym modelu wydają się być zbliżone do rozkładu normalnego. Jednoznaczną odpowiedź da jednak odpowiedni test.

ols_test_normality(wybrany_model)

-----------------------------------------------
       Test             Statistic       pvalue  
-----------------------------------------------
Shapiro-Wilk              0.868          0.0000 
Kolmogorov-Smirnov        0.1092         0.0000 
Cramer-von Mises         42.5504         0.0000 
Anderson-Darling         13.0233         0.0000 
-----------------------------------------------

Hipoteza zerowa w tych testach mówi o zgodności rozkładu reszt z rozkładem normalnym. Na podstawie wartości p, które są mniejsze od $\alpha=0,05$ stwierdzamy, że są podstawy do odrzucenia tej hipotezy czyli reszty z naszego modelu nie mają rozkładu normalnego. W diagnostyce przyczyn takiego stanu rzeczy pomoże nam wykres kwantyl-kwantyl:

ols_plot_resid_qq(wybrany_model)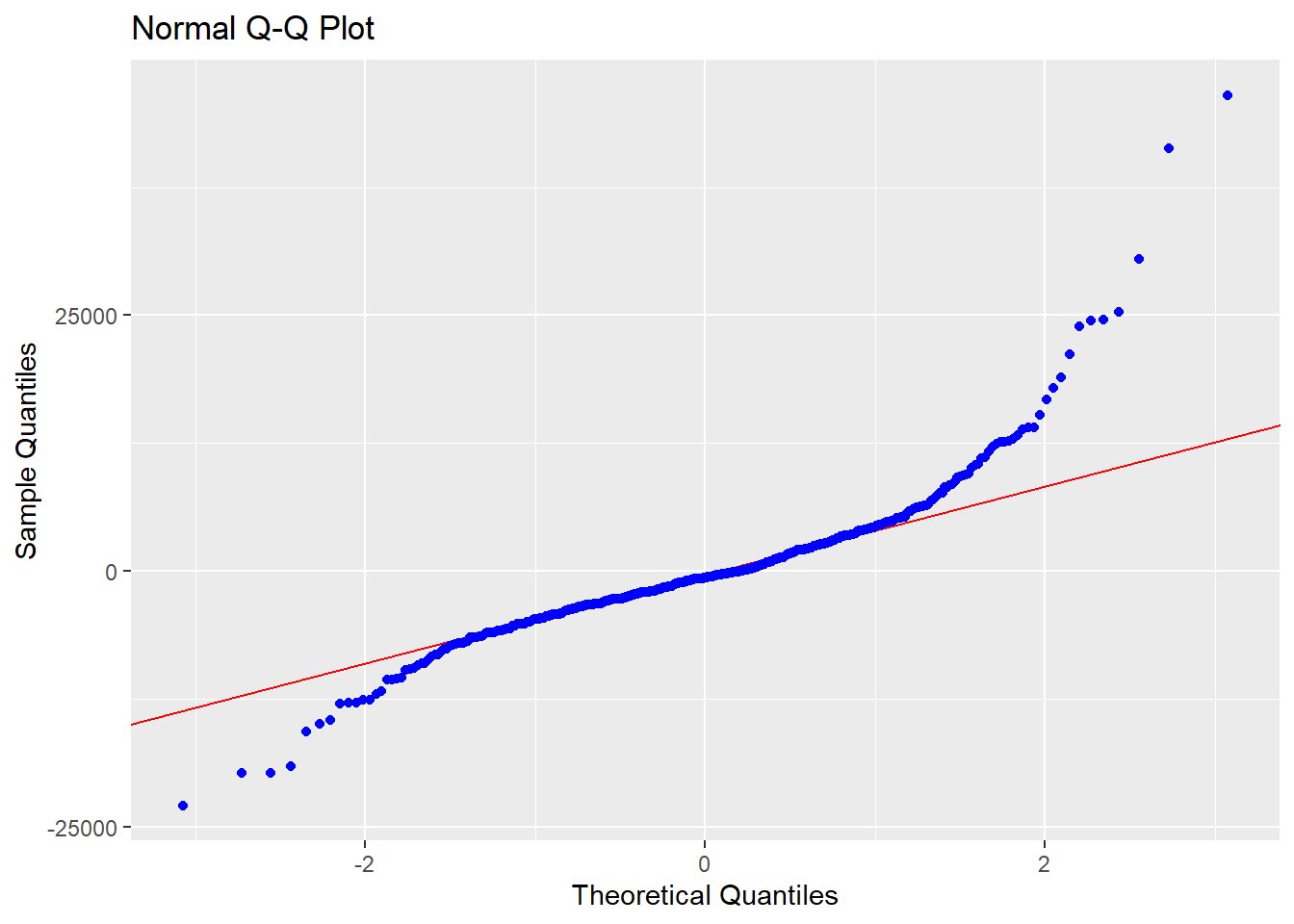

Gdyby wszystkie punkty leżały na prostej to oznaczałoby to normalność rozkładu reszt. Tymczasem po lewej i prawej stronie tego wykresu znajdują się potencjalne wartości odstające, które znacznie wpływają na rozkład reszt modelu.

Wartości odstające można ustalić na podstawie wielu kryteriów. Do jednych z najbardziej popularnych należy odległość Cooka:

cook <- ols_plot_cooksd_bar(wybrany_model)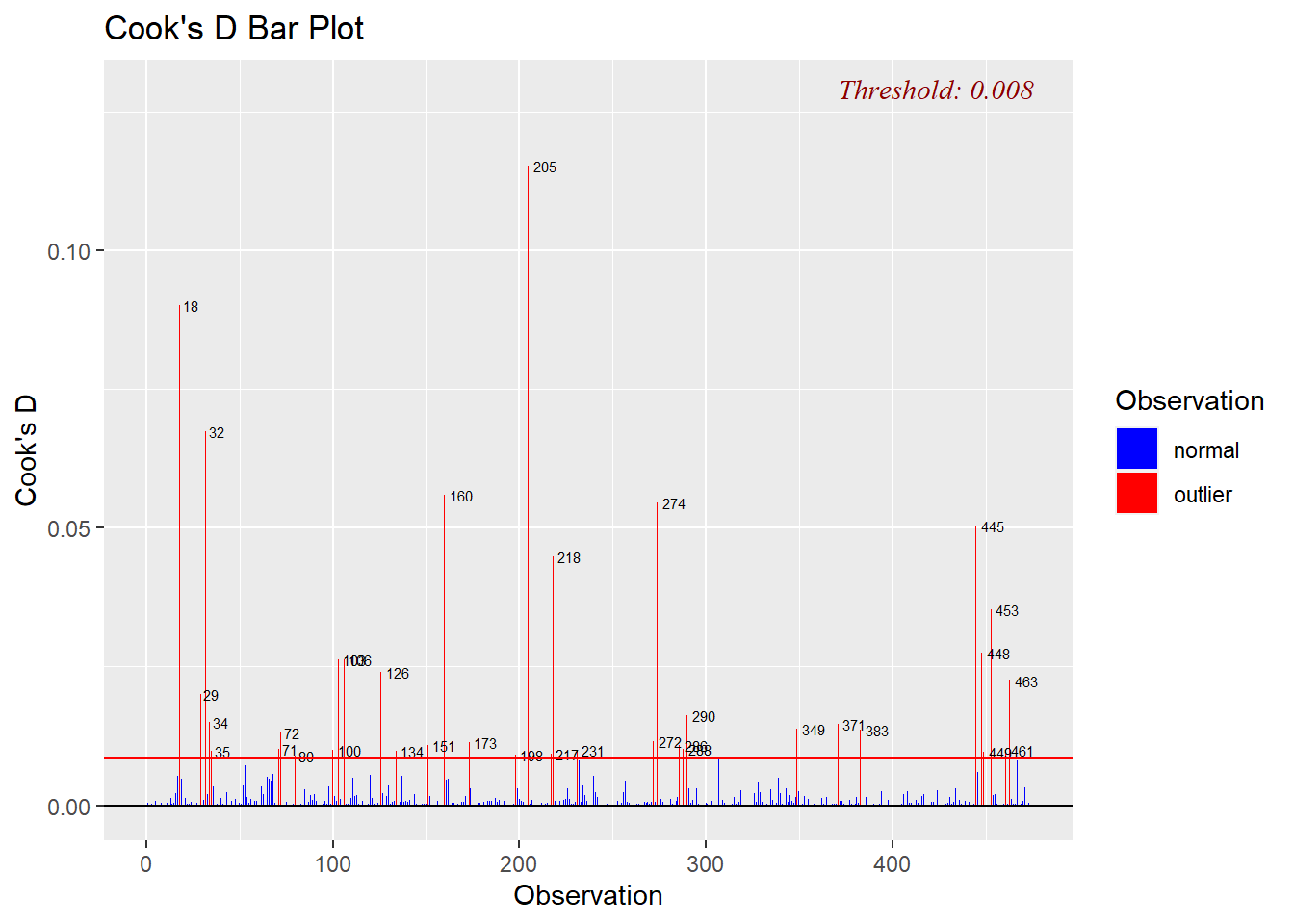

Przypisanie tej funkcji do obiektu zwraca nam tabelę z numerami zidentyfikowanych obserwacji wpływowych. W przypadku odległości Cooka jest to 35 obserwacji. Granica przynależności do grupy wartości odstających jest wyznaczana według wzoru: $4/n$, gdzie $n$ to liczba wszystkich obserwacji.

Inną miarą są reszty studentyzowane.

stud3 <- ols_plot_resid_stud(wybrany_model)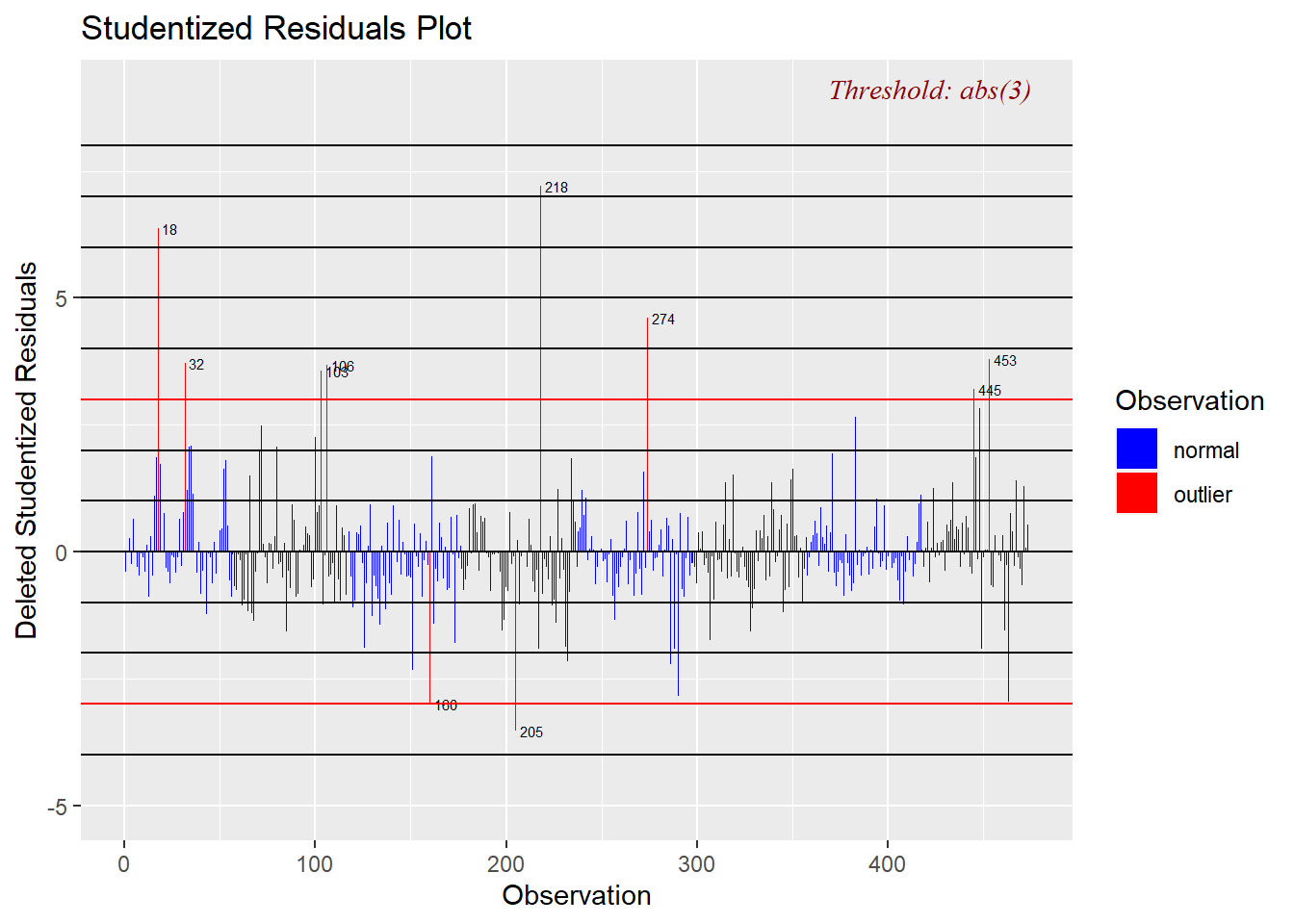

Wyżej wykorzystana funkcja jako kryterium odstawania przyjmuje wartość 3 identyfikując 10 obserwacji wpływowych. Z kolei dodanie do powyższej funkcji przyrostka fit powoduje przyjęcie jako granicy wartości równej 2.

stud2 <- ols_plot_resid_stud_fit(wybrany_model)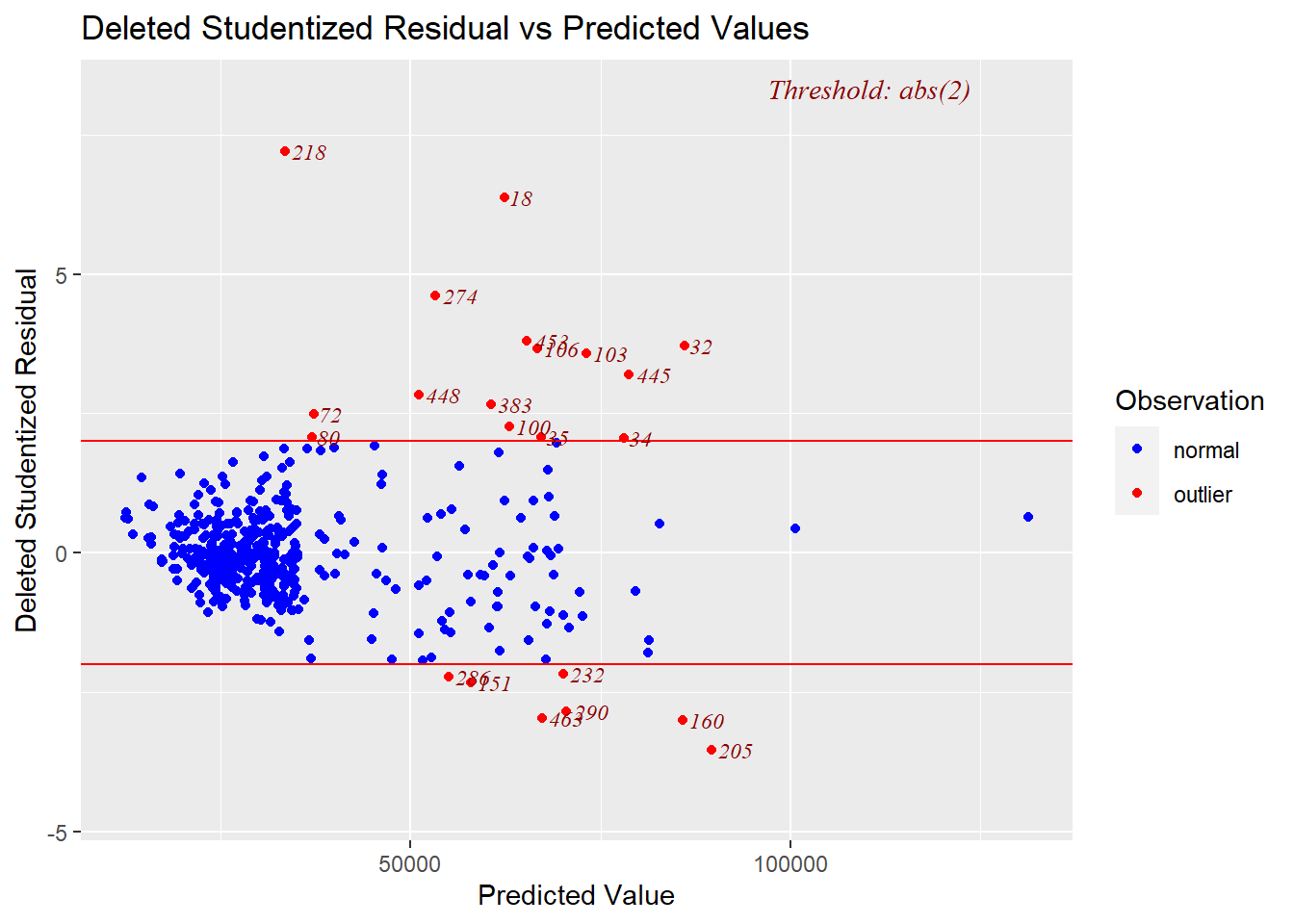

W ten sposób zostało zidentyfikowanych 22 obserwacji odstających. Korzystając z odległości Cooka wyeliminujemy obserwacje odstające ze zbioru:

outliers <- cook$data$obs[cook$data$color == "outlier"]

pracownicy_out <- pracownicy2[-outliers,]

wybrany_model_out <- lm(bwynagrodzenie ~ pwynagrodzenie + kat_pracownika + doswiadczenie + staz + plec + edukacja, 
                        data = pracownicy_out)
summary(wybrany_model_out)


Call:
lm(formula = bwynagrodzenie ~ pwynagrodzenie + kat_pracownika + 
    doswiadczenie + staz + plec + edukacja, data = pracownicy_out)

Residuals:
     Min       1Q   Median       3Q      Max 
-12591.2  -2696.4   -564.8   2263.0  14704.1 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)     -3756.8288  2381.5361  -1.577 0.115420    
pwynagrodzenie      1.3696     0.0676  20.260  < 2e-16 ***
kat_pracownika2  6480.6971  1049.9539   6.172 1.56e-09 ***
kat_pracownika3  9791.5000  1059.4980   9.242  < 2e-16 ***
doswiadczenie     -18.5808     2.3229  -7.999 1.17e-14 ***
staz              116.3809    20.9704   5.550 5.01e-08 ***
plec1           -1616.6030   505.1391  -3.200 0.001475 ** 
edukacja          397.7652   105.8146   3.759 0.000194 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4271 on 430 degrees of freedom
Multiple R-squared:  0.894, Adjusted R-squared:  0.8923 
F-statistic: 518.3 on 7 and 430 DF,  p-value: < 2.2e-16

Model dopasowany na takim zbiorze charakteryzuje się dużo mniejszym błędem standardowym oraz wyższym współczynnikiem $R^2$ w porównaniu do poprzedniego. Sprawdźmy w takim razie normalność reszt.

ols_plot_resid_qq(wybrany_model_out)

Wykres kwantyl-kwantyl wygląda już dużo lepiej i w zasadzie nie obserwuje tu się dużych odstępstw od rozkładu normalnego. Przeprowadźmy jeszcze odpowiednie testy statystyczne.

ols_test_normality(wybrany_model_out)

-----------------------------------------------
       Test             Statistic       pvalue  
-----------------------------------------------
Shapiro-Wilk              0.9696         0.0000 
Kolmogorov-Smirnov        0.0667         0.0405 
Cramer-von Mises         38.1644         0.0000 
Anderson-Darling          3.5421         0.0000 
-----------------------------------------------

Tylko test Kołmogorova-Smirnova na poziomie istotności $\alpha=0,01$ wskazał na brak podstaw do odrzucenia hipotezy zerowej.

4.3.1 Zadanie

Na podstawie zbioru dotyczącego 50 startupów określ jakie czynniki wpływają na przychód startupów.

startupy <- read_xlsx("data/startups.xlsx")

startupy <- janitor::clean_names(startupy)

summary(startupy)

   r_d_spend      administration   marketing_spend     state          
 Min.   :     0   Min.   : 51283   Min.   :     0   Length:50         
 1st Qu.: 39936   1st Qu.:103731   1st Qu.:129300   Class :character  
 Median : 73051   Median :122700   Median :212716   Mode  :character  
 Mean   : 73722   Mean   :121345   Mean   :211025                     
 3rd Qu.:101603   3rd Qu.:144842   3rd Qu.:299469                     
 Max.   :165349   Max.   :182646   Max.   :471784                     
     profit      
 Min.   : 14681  
 1st Qu.: 90139  
 Median :107978  
 Mean   :112013  
 3rd Qu.:139766  
 Max.   :192262